1. Bir çift hilesiz zar havaya atılıyor. En az bir zarın 5 gelmesi olayının eleman sayısı aşağıdakilerden hangisidir?
A) 12
B) 11
C) 5
D) 10
E) 6
Cevap : B) 11
Açıklama : İki zar atıldığında toplam 36 durum vardır. Hiç 5 gelmeme durumu (5 dışındaki 5 rakamın gelmesi)  ‘tir. Tüm durumlardan hiç 5 gelmeme durumunu çıkarırsak: ‘tir. Tüm durumlardan hiç 5 gelmeme durumunu çıkarırsak:  bulunur. bulunur.
2.  matrisinin matrisinin  girdisinin kofaktörü aşağıdakilerden hangisidir? girdisinin kofaktörü aşağıdakilerden hangisidir?
A) 2
B) -2
C) 5
D) 4
E) -4
Cevap : E) -4
Açıklama :  elemanı 3. satır 2. sütundadır. Kofaktör işareti elemanı 3. satır 2. sütundadır. Kofaktör işareti  ‘dir. Minor matrisi (3. satır ve 2. sütun kapatıldığında): ‘dir. Minor matrisi (3. satır ve 2. sütun kapatıldığında):  . Kofaktör: . Kofaktör:  . .
3.  matrisinin rankı ( matrisinin rankı (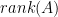 ) aşağıdakilerden hangisidir? ) aşağıdakilerden hangisidir?
A) 0
B) 2
C) 1
D) 3
E) 4
Cevap : D) 3
Açıklama : Satır işlemleri yapıldığında, satırların lineer bağımsız olduğu görülür ve matrisin rankı 3 olarak bulunur.
4. x, y, z ve t birbirlerinden farklı elemanlar olmak üzere  kümesi üzerinde tanımlanan bir kümesi üzerinde tanımlanan bir  bağıntısı için aşağıdakilerden hangisi doğrudur? bağıntısı için aşağıdakilerden hangisi doğrudur?
A) R bir fonksiyondur.
B) Anti-simetriktir.
C) Geçişmelidir.
D) R simetrik değildir.
E) R yansımalıdır.
Cevap : D) R simetrik değildir.
Açıklama : Simetrik olması için her  için için  olmalıdır. Bağıntıda olmalıdır. Bağıntıda  var ancak var ancak  yoktur. Bu yüzden simetrik değildir. yoktur. Bu yüzden simetrik değildir.
5.  matrisinin transpozesi matrisinin transpozesi ![A^{T}=[a_{ij}]](https://s0.wp.com/latex.php?latex=A%5E%7BT%7D%3D%5Ba_%7Bij%7D%5D&bg=ffffff&fg=000&s=0&c=20201002) olmak üzere olmak üzere 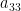 girdisi aşağıdakilerden hangisidir? girdisi aşağıdakilerden hangisidir?
A) 4
B) 5
C) 0
D) 2
E) 3
Cevap : C) 0
Açıklama : Cevap anahtarı C (0) olarak verilmiştir. Ancak matrisin transpozu alındığında  elemanı normalde 5’tir (orijinal matrisin 3. satır 3. sütunu). Cevap anahtarının 0 olması, sorunun muhtemelen transpozun elemanı normalde 5’tir (orijinal matrisin 3. satır 3. sütunu). Cevap anahtarının 0 olması, sorunun muhtemelen transpozun  elemanını (orijinal matrisin elemanını (orijinal matrisin  elemanı olan 0) sormayı amaçladığını düşündürmektedir. Resmi cevap anahtarına göre cevap C’dir. elemanı olan 0) sormayı amaçladığını düşündürmektedir. Resmi cevap anahtarına göre cevap C’dir.
6.  fonksiyonunun türevi aşağıdakilerden hangisidir? fonksiyonunun türevi aşağıdakilerden hangisidir?
A) 
B) 
C) 
D) 
E) 
Cevap : A) 
Açıklama :  olarak yazılır. Türev: olarak yazılır. Türev:  . .
7.  üzerinde üzerinde  eşitliğini sağlayan x, y, z reel sayıları sırasıyla aşağıdakilerden hangisidir? eşitliğini sağlayan x, y, z reel sayıları sırasıyla aşağıdakilerden hangisidir?
A) -2, 3, 1/3
B) 3, -3, 3/2
C) 3, -3, -2
D) -3, 3, 3/2
E) -1, 3, 1/2
Cevap : D) -3, 3, 3/2
Açıklama :  . .  . .  . .
8.  ve ve  matrisleri için BA çarpım matrisi için aşağıdakilerden hangisi doğrudur? matrisleri için BA çarpım matrisi için aşağıdakilerden hangisi doğrudur?
A) 
B) 
C) Tanımlı değildir.
D) 
E) 
Cevap : C) Tanımlı değildir.
Açıklama : B matrisi  , A matrisi , A matrisi 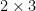 boyutundadır. BA çarpımı için B’nin sütun sayısı (4) ile A’nın satır sayısının (2) eşit olması gerekir. boyutundadır. BA çarpımı için B’nin sütun sayısı (4) ile A’nın satır sayısının (2) eşit olması gerekir.  olduğu için çarpım tanımlı değildir. olduğu için çarpım tanımlı değildir.
9. p: “Mars bir gezegendir” ve q: “Türkiye bir ada değildir.” iki önerme olmak üzere  önermesinin ifadesi aşağıdakilerden hangisidir? önermesinin ifadesi aşağıdakilerden hangisidir?
A) Mars bir gezegen ise Türkiye bir ada değildir.
B) Mars bir gezegen ise Türkiye bir adadır.
C) Mars bir gezegendir ve Türkiye bir adadır.
D) Mars bir gezegen değildir ve Türkiye bir ada değildir.
E) Mars bir gezegendir veya Türkiye bir ada değildir.
Cevap : B) Mars bir gezegen ise Türkiye bir adadır.
Açıklama : q önermesinin değili (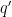 ) “Türkiye bir adadır” olur. ) “Türkiye bir adadır” olur.  ifadesi “Mars bir gezegen ise Türkiye bir adadır” şeklinde okunur. ifadesi “Mars bir gezegen ise Türkiye bir adadır” şeklinde okunur.
10.  limitinin sonucu aşağıdakilerden hangisidir? limitinin sonucu aşağıdakilerden hangisidir?
A) 2/3
B) 0
C) 1
D) 1/2
E) Sonsuz
Cevap : A) 2/3
Açıklama : Belirsizlik durumunda L’Hopital kuralı uygulanır:  . x=0 için . x=0 için  . .
11. Dağılımı 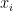 değerleri için 2, 3, 11 ve olasılıkları değerleri için 2, 3, 11 ve olasılıkları 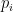 sırasıyla sırasıyla 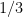 , , 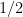 , , 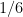 gibi olan bir X rastgele değişkeninin beklenen değeri aşağıdakilerden hangisidir? gibi olan bir X rastgele değişkeninin beklenen değeri aşağıdakilerden hangisidir?
A) 3.2
B) 10
C) 12
D) 26
E) 4
Cevap : E) 4
Açıklama : Beklenen değer ![E[X] = \sum x_i \cdot p_i = 2(1/3) + 3(1/2) + 11(1/6) = 4/6 + 9/6 + 11/6 = 24/6 = 4](https://s0.wp.com/latex.php?latex=E%5BX%5D+%3D+%5Csum+x_i+%5Ccdot+p_i+%3D+2%281%2F3%29+%2B+3%281%2F2%29+%2B+11%281%2F6%29+%3D+4%2F6+%2B+9%2F6+%2B+11%2F6+%3D+24%2F6+%3D+4&bg=ffffff&fg=000&s=0&c=20201002) . .
12.  , ,  , ,  lineer denklem sisteminin serbest değişkenleri aşağıdakilerden hangisidir? lineer denklem sisteminin serbest değişkenleri aşağıdakilerden hangisidir?
A) 
B) 
C) Sistemin serbest değişkeni yoktur.
D) 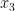
E) 
Cevap : C) Sistemin serbest değişkeni yoktur.
Açıklama : Üçgen matris formunda olan bu sistemde her değişkene karşılık gelen bir pivot (katsayı) bulunduğu için serbest değişken yoktur, tek çözüm vardır.
13.  ‘in ‘in  ve ve  vektörleri için vektörleri için  iç çarpımı aşağıdakilerden hangisidir? iç çarpımı aşağıdakilerden hangisidir?
A) 51
B) 23
C) 0
D) -5
E) 5
Cevap : D) -5
Açıklama :  . .
14. x, y, z, t reel sayılar olmak üzere  matrisinin klasik eşleniği (ek matrisi/adjoint) aşağıdakilerden hangisidir? matrisinin klasik eşleniği (ek matrisi/adjoint) aşağıdakilerden hangisidir?
A) 
B) 
C) 
D) 
E) 
Cevap : A) 
Açıklama : 2×2 matrisin ek matrisi bulunurken, ana köşegen elemanları yer değiştirir (x ve t), yedek köşegen elemanları işaret değiştirir (y ve z).
15. İki çocuğa sahip bir çiftin büyük çocuğu erkek ise her iki çocuğun da erkek olma olasılığı hangisidir?
A) 1/3
B) 1/2
C) 3/4
D) 1/4
E) 1
Cevap : B) 1/2
Açıklama : Örnek uzay (Büyük, Küçük): {EE, EK}. Büyük çocuğun erkek olduğu bilindiğine göre olası durumlar bunlardır. İkisinin de erkek olduğu durum sadece {EE}’dir. Olasılık 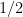 . .
16. A, Bilgisayar Programlama bölümündeki öğrencilerin kümesi ve B, Bilgisayar Programlama bölümündeki gözlük takan öğrencilerin kümesi olmak üzere  kümesi aşağıdakilerden hangisidir? kümesi aşağıdakilerden hangisidir?
A) Bilgisayar Programlama bölümündeki gözlük takan öğrencilerin kümesi
B) Bilgisayar Programlama bölümüne kayıtlı olmayan öğrencilerin kümesi
C) Bilgisayar Programlama bölümündeki kız öğrencilerin kümesi
D) Bilgisayar Programlama bölümündeki gözlük takmayan öğrencilerin kümesi
E) Bilgisayar Programlama bölümündeki öğrencilerin kümesi
Cevap : A) Bilgisayar Programlama bölümündeki gözlük takan öğrencilerin kümesi
Açıklama : B kümesi A kümesinin alt kümesidir. Kesişimleri alt küme olan B’ye eşittir.
17.  fonksiyonunun türevinin fonksiyonunun türevinin 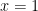 noktasındaki değeri aşağıdakilerden hangisidir? noktasındaki değeri aşağıdakilerden hangisidir?
A) 1/2
B) 0
C) 1
D) 3/2
E) -1/2
Cevap : E) -1/2
Açıklama :  . Türev: . Türev:  . x=1 için: . x=1 için:  . .
18. Doğal sayılar kümesinden reel sayılar kümesine tanımlı bir f fonksiyonu n tek bir doğal sayı ise  değerini, n çift bir doğal sayı ise değerini, n çift bir doğal sayı ise  değerini alsın. f fonksiyonu için aşağıdakilerden hangisi doğrudur? değerini alsın. f fonksiyonu için aşağıdakilerden hangisi doğrudur?
A) Tersi vardır.
B) Ne birebir ne de üzerinedir.
C) Birebir ama üzerine değildir.
D) Birebir değil ama üzerinedir.
E) Birebir ve üzerinedir.
Cevap : C) Birebir ama üzerine değildir.
Açıklama : Fonksiyon tam sayıları üretir ancak Reel sayılar kümesini (örneğin 1/2, 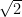 gibi sayıları) örtmez, bu yüzden üzerine değildir. Her n değeri farklı bir sonuç ürettiği için birebirdir. gibi sayıları) örtmez, bu yüzden üzerine değildir. Her n değeri farklı bir sonuç ürettiği için birebirdir.
19.  matrisinin determinantı aşağıdakilerden hangisidir? matrisinin determinantı aşağıdakilerden hangisidir?
A) -88
B) 146
C) 214
D) -45
E) -131
Cevap : E) -131
Açıklama : Matrisin determinantı hesaplandığında sonuç -131 bulunur.
20.  eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir? eşitsizliğinin çözüm kümesi aşağıdakilerden hangisidir?
A) {-5, 7}
B) [-5/6, 3/2]
C) [-5, 7]
D) [5/3, 7/3]
E) (-1/3, 2/3)
Cevap : B) [-5/6, 3/2]
Açıklama :  . .
|




