1.  , ,  , ,  lineer denklem sistemiyle ilgili aşağıdakilerden hangisi doğrudur? lineer denklem sistemiyle ilgili aşağıdakilerden hangisi doğrudur?
A) Tek çözümü vardır.
B) Sonsuz sayıda çözümü vardır.
C) Sıfır çözümü vardır.
D) Çözümü yoktur.
E) (0, 1, 2) bir çözümüdür.
Cevap : B) Sonsuz sayıda çözümü vardır.
Açıklama : Denklem sisteminin katsayılar matrisinin determinantı 0’dır ve 3. denklem, 1. denklem ile 2. denklemin 2 katının toplamına eşittir ( ). Bu durum, denklemlerin lineer bağımlı olduğunu ve sistemin sonsuz sayıda çözümü olduğunu gösterir. ). Bu durum, denklemlerin lineer bağımlı olduğunu ve sistemin sonsuz sayıda çözümü olduğunu gösterir.
2.  ‘in ‘in  vektörünün vektörünün  vektörü üzerine izdüşümü aşağıdakilerden hangisidir? vektörü üzerine izdüşümü aşağıdakilerden hangisidir?
A) 
B) 
C) 0
D) 
E) 
Cevap : D) 
Açıklama : İzdüşüm formülü  dir. İç çarpım dir. İç çarpım  ve ve  olarak hesaplanır. Sonuç olarak hesaplanır. Sonuç  olur. olur.
3. Bir kolide bulunan 13 yumurtadan 5 tanesi bozuktur. Bu koliden rastgele 4 yumurta seçilmektedir ve seçilen yumurtalar koliye tekrar konmamaktadır. Seçilen 4 yumurtadan tümünün bozuk olma olasılığı aşağıdakilerden hangisidir?
A) 
B) 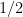
C) 
D) 
E) 
Cevap : A) 
Açıklama : 5 bozuk yumurtadan 4’ünü seçme kombinasyonu  , toplam 13 yumurtadan 4’ünü seçme kombinasyonu , toplam 13 yumurtadan 4’ünü seçme kombinasyonu  ‘tür. ‘tür.  sonucuna ulaşılır. sonucuna ulaşılır.
4.  vektörünün uzunluğu aşağıdakilerden hangisidir? vektörünün uzunluğu aşağıdakilerden hangisidir?
A) 25
B) 
C) 13
D) 
E) 38
Cevap : D) 
Açıklama : Vektör uzunluğu  dir. dir.
5. Aşağıdakilerden hangisi bir önerme değildir?
A)  dir. dir.
B) İtalya’nın başkenti Roma’dır.
C)  dir. dir.
D) Bugün hava güneşlidir.
E) Su içmek bir ihtiyaç mıdır?
Cevap : E) Su içmek bir ihtiyaç mıdır?
Açıklama : Soru cümleleri, bir yargı (doğru veya yanlış) bildirmediği için mantıkta önerme olarak kabul edilmez.
6. Hilesiz iki zar aynı anda havaya atılıyor. Zarlardan birinin 4’ten büyük geldiği bilindiğine göre üst yüzeye gelen sayıların toplamının 5 olma olasılığı aşağıdakilerden hangisidir?
A) 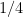
B) 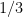
C) 0
D) 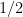
E) 
Cevap : C) 0
Açıklama : Toplamı 5 olan zar çiftleri (1,4), (2,3), (3,2), (4,1)’dir. Bu çiftlerin hiçbirinde zarlardan biri 4’ten büyük (5 veya 6) değildir. Bu nedenle verilen koşul altında bu olasılık 0’dır.
7.  fonksiyonu için fonksiyonu için  aşağıdakilerden hangisidir? aşağıdakilerden hangisidir?
A) 32
B) 225
C) 240
D) -240
E) -15
Cevap : D) -240
Açıklama : Zincir kuralı ile türev:  . . 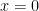 için için  . .
8.  ve ve  olmak üzere olmak üzere  değeri aşağıdakilerden hangisidir? değeri aşağıdakilerden hangisidir?
A) -2
B) -1
C) 5
D) 4
E) 0
Cevap : A) -2
Açıklama :  . Önce . Önce  . Sonra . Sonra  . .
9.  fonksiyonu için fonksiyonu için  aşağıdakilerden hangisidir? aşağıdakilerden hangisidir?
A) -2
B) -1
C) -4
D) 0
E) 2
Cevap : E) 2
Açıklama : Türev  . . 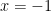 yerine konulursa yerine konulursa  . .
10.  ve ve  olmak üzere olmak üzere  işleminin sonucu aşağıdakilerden hangisidir? işleminin sonucu aşağıdakilerden hangisidir?
A) 
B) 
C) 
D) 
E) 
Cevap : B) 
Açıklama : Simetrik fark işlemi, her iki kümenin kesişimi olan  elemanlarının atılmasıyla, sadece A’da ve sadece B’de olan elemanların birleşimidir. elemanlarının atılmasıyla, sadece A’da ve sadece B’de olan elemanların birleşimidir.
11.  kümesi üzerinde tanımlı kümesi üzerinde tanımlı  bağıntısına göre A kümesinin parçalanışı aşağıdakilerden hangisidir? bağıntısına göre A kümesinin parçalanışı aşağıdakilerden hangisidir?
A) 
B) 
C) 
D) 
E) 
Cevap : E) 
Açıklama : Bağıntıdaki eşleşmelere bakıldığında; 1 ve 5 kendi arasında, 2, 3 ve 6 kendi arasında ilişkilidir. 4 ise sadece kendisiyle ilişkilidir. Bu durum E şıkkındaki denklik sınıflarını oluşturur.
12.  limitinin değeri aşağıdakilerden hangisidir? limitinin değeri aşağıdakilerden hangisidir?
A) -8
B) 
C) 8
D) 0
E) -1
Cevap : D) 0
Açıklama :  değeri yerine yazıldığında değeri yerine yazıldığında  sonucu elde edilir. Belirsizlik yoktur. sonucu elde edilir. Belirsizlik yoktur.
|




