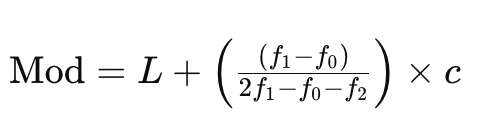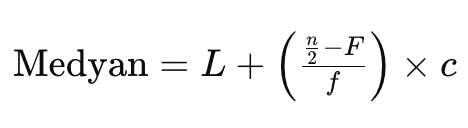İstatistik Ünite -7
Verilerin Özetlenmesi: Analitik Olmayan Ortalamalar
#1. Sıralanmış bir seride tam ortada yer alan değere ———- denir.
Cevap : C) Medyan
Açıklama : Medyan, sıralanmış bir seride tam ortada yer alan değeri ifade eder.
#2. Pozitif asimetri bir seri için aşağıdakilerden hangisi doğrudur?
Cevap : C) Mod<Medyan
Açıklama : Pozitif asimetrik bir seride, aritmetik ortalama en büyüktür, mod ise en küçüktür.
#3.
Aşağıda verilen sınıflanmış seride medyan sınıfı hangi sınıftır?
Sınıflar:
0-10 (4),
10-20 (9),
20-30 (8),
30-40 (7),
40-50 (6)
Cevap : E) 20-30 sınıfı
Açıklama : Medyan sınıfı, gözlem değerlerinin yarısının bulunduğu sınıftır. Bu sınıfta 20-30 sınıfı yer alır.
#4.
Aşağıda verilen sınıflanmış seride mod sınıfı hangi sınıftır?
| Sınıflar | nᵢ |
| 0-10 | 4 |
| 10-20 | 9 |
| 20-30 | 8 |
| 30-40 | 7 |
| 40-50 | 6 |
Cevap : B) 10-20 sınıfı
Açıklama : Mod sınıfı en yüksek frekansa sahip olan sınıftır. 10-20 sınıfı 9 frekansla en yüksek değere sahiptir.
#5.
Aşağıda verilen serinin modu nedir?
| Xᵢ | nᵢ |
| 10 | 5 |
| 20 | 7 |
| 25 | 9 |
| 30 | 7 |
| 40 | 5 |
Cevap : A) 25
Açıklama : Mod en çok tekrar eden değerdir. Verilen seride en yüksek frekans 25’tir.
Öğrenci Dostu Öğrenme Yönetim Sistemi Lolonolo, bol bol test yapmayı önerir.
#6. Bir sınıfta bulunan 10 öğrencinin ağırlıkları
65, 70, 70, 60, 55, 60, 70, 60, 65, 60
olarak ölçülmüştür.
Buna göre ağırlıkların mod değeri nedir?
Cevap : A) 60
Açıklama : 60 değeri seride en çok tekrar eden değerdir, bu yüzden mod 60’tır.
#7. Seride yer alan gözlem değerleri arasında en çok tekrar eden gözlem değerine ———- denir.
Cevap : A) Mod
Açıklama : Mod, seride en çok tekrar eden gözlem değeridir.
#8. Aşağıdaki ortalamalardan hangisi analitik olmayan (duyarsız) bir ortalamadır?
Cevap: C) Medyan
Açıklama: Medyan, sıralı bir veri setinde ortada yer alan değeri temsil eden duyarsız bir ortalamadır. Tüm gözlem değerleri hesaba katılmaz, sadece sıralanmış verilerin ortasında bulunan değere odaklanılır.
#9. Gözlem değerleri
(2, 3, 5, 6, 7, 7, 8, 8, 8, 9, 9, 10)
olan ve 12 gözlemden oluşan serinin medyanı nedir?
Cevap : C) 7,5
Açıklama : Ortadaki iki değer (7 ve 8)’in aritmetik ortalaması medyanı verir: (7 8) / 2 = 7,5.
#10. Simetrik bir seri için aşağıdakilerden hangisi doğrudur?
Cevap : C) Aritmetik Ortalama=Medyan=Mod
Açıklama : Simetrik bir dağılımda, Aritmetik Ortalama, Medyan ve Mod aynı değeri alır.
Öğrenci Dostu Öğrenme Yönetim Sistemi Lolonolo, bol bol test yapmayı önerir.
SONUÇ
İstatistik Ünite -7
Verilerin Özetlenmesi: Analitik Olmayan Ortalamalar
İstatistik Ünite -7
Verilerin Özetlenmesi: Analitik Olmayan Ortalamalar
HD Quiz powered by harmonic design
İstatistik Ünite -7
Verilerin Özetlenmesi: Analitik Olmayan Ortalamalar
Verilerin Özetlenmesi: Analitik Olmayan Ortalamalar |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
@lolonolo_com |
Verilerin Özetlenmesi: Analitik Olmayan Ortalamalar |
|||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
@lolonolo_com |
Auzef TDS 1. Sınıf Güz Dönemi
çıkmış sınav soruları
Verilerin Özetlenmesi: Analitik Olmayan Ortalamalar
 |
 |
 |
 |
—
İstatistik Ünite -7
Verilerin Özetlenmesi: Analitik Olmayan Ortalamalar
Tıbbi Dokğmantason Ve Sekreterlik 1. Sınıf Güz Döenmi
Auzef Çocuk Gelişimi 1. sınıf bahar dönemi
—